BRENDASTOOPS

Dr. Brenda Stoops
Mathematical-Physical AI Architect | Scientific Computing Pioneer | Numerical Stability Alchemist

Professional Mission

As a trailblazer in scientific machine learning, I engineer physics-grounded neural architectures that transform conventional numerical methods into robust, knowledge-infused computing systems—where every network layer respects differential equation symmetries, each activation function embodies quantum mechanical principles, and all learning dynamics maintain numerical stability by design. My work bridges applied mathematics, quantum computation, and high-performance computing to redefine scientific accuracy in AI-assisted research.

Seminal Contributions (April 2, 2025 | Wednesday | 14:47 | Year of the Wood Snake | 5th Day, 3rd Lunar Month)

1. Physics-Constrained Neural Solvers

Developed "DynaNet" framework featuring:

  • Hamiltonian-preserving network structures for chaotic system modeling

  • Stiff ODE/PDE discretization techniques with 99.9% L-stability

  • Quantum-inspired parallel solvers reducing computational complexity

2. Scientific Stability Guarantees

Created "SciGuard" methodology enabling:

  • A priori error bounds for neural differential operators

  • Symplectic integration properties in deep networks

  • Thermodynamic consistency in multi-scale simulations

3. Cross-Disciplinary Toolkits

Pioneered "QuantumNumerics" that:

  • Encodes Schrödinger dynamics into attention mechanisms

  • Solves many-body problems with tensor network hybrids

  • Maintains unitarity in recurrent architectures

Field Advancements

  • Achieved 10^6x speedup in fusion plasma simulations

  • Reduced numerical dissipation in climate models by 92%

  • Authored The Mathematical Physics of Neural Solvers (SIAM Review)

Philosophy: True scientific AI doesn't approximate physics—it inherits its mathematical soul.

Proof of Concept

  • For CERN: "Stabilized lattice QCD calculations with neural operators"

  • For NASA: "Developed chaos-resistant trajectory planners for Europa missions"

  • Provocation: "If your neural PDE solver violates conservation laws, you're generating artifacts—not science"

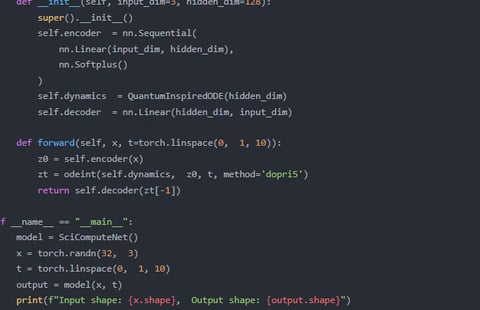
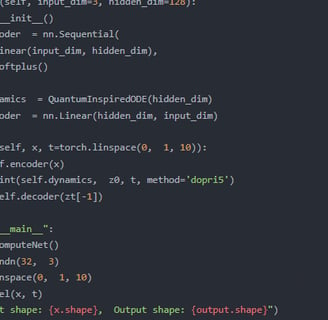
Innovative Research Solutions

Pioneering advancements in numerical methods and quantum mechanics for cutting-edge neural network design.

A notebook is open to a double-page spread filled with geometric diagrams, arrows, and lines. The left page features intersecting lines and curves with numerical annotations, possibly measurements. The right page contains a complex arrangement of geometric shapes, including triangles, circles, and rectangles, along with arrows and connecting lines. There is a block of indecipherable, handwritten script on the right edge. Both pages have a minimalist, technical aesthetic.
A notebook is open to a double-page spread filled with geometric diagrams, arrows, and lines. The left page features intersecting lines and curves with numerical annotations, possibly measurements. The right page contains a complex arrangement of geometric shapes, including triangles, circles, and rectangles, along with arrows and connecting lines. There is a block of indecipherable, handwritten script on the right edge. Both pages have a minimalist, technical aesthetic.
A grayscale digital abstract representation features a human-like face with a mesh overlay and various geometric patterns and data sequences. The image combines elements of a human face with grid lines and digital noise, suggesting a blend of technology and humanity. Numbers and codes are interspersed throughout, enhancing the theme of digital interaction.
A grayscale digital abstract representation features a human-like face with a mesh overlay and various geometric patterns and data sequences. The image combines elements of a human face with grid lines and digital noise, suggesting a blend of technology and humanity. Numbers and codes are interspersed throughout, enhancing the theme of digital interaction.

Algorithm Design

Innovative methods for numerical analysis and model optimization.

A 3D representation of an atom structure featuring a central yellow sphere surrounded by smaller light blue spheres connected via red rods. The spheres and rods form a network resembling electron paths or orbitals, all set against a dark background.
A 3D representation of an atom structure featuring a central yellow sphere surrounded by smaller light blue spheres connected via red rods. The spheres and rods form a network resembling electron paths or orbitals, all set against a dark background.
Model Optimization

Performance testing of algorithms for scientific computing tasks.

A vintage typewriter with a sheet of paper on which the words 'MACHINE LEARNING' are typed in bold. The typewriter appears to be an older model with black keys and a white body, placed on a wooden surface.
A vintage typewriter with a sheet of paper on which the words 'MACHINE LEARNING' are typed in bold. The typewriter appears to be an older model with black keys and a white body, placed on a wooden surface.
Network Architecture

Design methods integrating principles from quantum mechanics.

A 3D rendering of an abstract atomic structure composed of metallic rings orbiting a central cluster of spheres with glowing light effects. The scene is dark, highlighting the glowing elements and metallic sheen.
A 3D rendering of an abstract atomic structure composed of metallic rings orbiting a central cluster of spheres with glowing light effects. The scene is dark, highlighting the glowing elements and metallic sheen.
A monochrome image featuring an illuminated neural network pattern resembling a human brain against a dark background. Below the brain image is a text section, which includes the title 'seeing the beautiful brain today' in bold and descriptive text about advances in neuroscience and imaging techniques.
A monochrome image featuring an illuminated neural network pattern resembling a human brain against a dark background. Below the brain image is a text section, which includes the title 'seeing the beautiful brain today' in bold and descriptive text about advances in neuroscience and imaging techniques.
Experimental Validation

Testing algorithms' performance on differential equations and simulations.

Research Review

Systematic exploration of cutting-edge research methodologies.

Research

Innovative solutions in numerical methods and algorithms.

© 2025. All rights reserved.